What is an "i j k vector"? An "i j k vector" is an ordered triple of numbers that represent the coordinates of a point in three-dimensional space. The letters "i", "j", and "k" are used to represent the unit vectors in the x, y, and z directions, respectively.
For example, the vector (3, 4, 5) represents the point that is 3 units to the right of the origin, 4 units up from the origin, and 5 units out of the page.
Vectors are used in a wide variety of applications, including physics, engineering, and computer graphics. They can be used to represent forces, velocities, positions, and many other quantities.
The concept of vectors was first developed by the Italian mathematician and physicist Giambattista Benedetti in the 16th century. However, it was not until the 19th century that vectors were fully developed and their importance was recognized.
i j k vector
An "i j k vector" is an ordered triple of numbers that represent the coordinates of a point in three-dimensional space. The letters "i", "j", and "k" are used to represent the unit vectors in the x, y, and z directions, respectively. Vectors are used in a wide variety of applications, including physics, engineering, and computer graphics.
- Coordinate system
- Vector addition and subtraction
- Scalar multiplication
- Dot product
- Cross product
These key aspects of i j k vectors are essential for understanding their use in various applications. For example, in physics, vectors are used to represent forces, velocities, and positions. In engineering, vectors are used to represent forces, moments, and stresses. In computer graphics, vectors are used to represent points, lines, and polygons.
Coordinate system
A coordinate system is a system that uses one or more numbers, called coordinates, to uniquely determine the position of a point or other geometric element. The most common coordinate system is the Cartesian coordinate system, which uses three numbers, called the x-coordinate, y-coordinate, and z-coordinate, to determine the position of a point in three-dimensional space.
- Axes
The Cartesian coordinate system is defined by three axes, which are perpendicular to each other. The x-axis points to the right, the y-axis points up, and the z-axis points out of the page. Points in the Cartesian coordinate system are represented by their coordinates, which are the distances from the point to each of the axes.
- Origin
The origin of the Cartesian coordinate system is the point where all three axes intersect. The coordinates of the origin are (0, 0, 0).
- Units
The units of the Cartesian coordinate system are determined by the application. For example, in physics, the units of the Cartesian coordinate system might be meters. In computer graphics, the units of the Cartesian coordinate system might be pixels.
- Transformations
Points in the Cartesian coordinate system can be transformed using a variety of transformations, such as translation, rotation, and scaling. Transformations are used to move, rotate, and scale objects in three-dimensional space.
The Cartesian coordinate system is a powerful tool for representing and manipulating points in three-dimensional space. It is used in a wide variety of applications, including physics, engineering, and computer graphics.
Vector addition and subtraction
Vector addition and subtraction are two basic operations that can be performed on vectors. Vector addition is the operation of adding two vectors together to produce a new vector. Vector subtraction is the operation of subtracting one vector from another to produce a new vector.
- Adding vectors
To add two vectors, we simply add their corresponding coordinates. For example, the vector (1, 2, 3) + (4, 5, 6) = (5, 7, 9).
- Subtracting vectors
To subtract one vector from another, we simply subtract the corresponding coordinates. For example, the vector (1, 2, 3) - (4, 5, 6) = (-3, -3, -3).
- Geometric interpretation
Vector addition and subtraction can be interpreted geometrically. Vector addition corresponds to the parallelogram law of vector addition, which states that the resultant vector of two vectors is the diagonal of the parallelogram that has the two vectors as its sides. Vector subtraction corresponds to the triangle law of vector subtraction, which states that the resultant vector of two vectors is the vector that points from the tail of the first vector to the head of the second vector.
- Applications
Vector addition and subtraction are used in a wide variety of applications, including physics, engineering, and computer graphics. In physics, vector addition and subtraction are used to calculate the resultant force acting on an object. In engineering, vector addition and subtraction are used to calculate the resultant moment acting on a body. In computer graphics, vector addition and subtraction are used to translate and rotate objects.
Vector addition and subtraction are two fundamental operations that are used in a wide variety of applications. They are essential for understanding the behavior of vectors and for solving problems in physics, engineering, and computer graphics.
Scalar multiplication
Scalar multiplication is a mathematical operation that multiplies a vector by a scalar. A scalar is a quantity that has only magnitude, not direction. In the context of i j k vectors, scalar multiplication is used to scale the vector by a certain factor.
- Scaling a vector
Scalar multiplication can be used to scale a vector by a certain factor. For example, if we multiply the vector (1, 2, 3) by the scalar 2, we get the vector (2, 4, 6). This means that the new vector is twice as long as the original vector.
- Changing the direction of a vector
Scalar multiplication can also be used to change the direction of a vector. For example, if we multiply the vector (1, 2, 3) by the scalar -1, we get the vector (-1, -2, -3). This means that the new vector points in the opposite direction of the original vector.
- Applications
Scalar multiplication is used in a variety of applications, including physics, engineering, and computer graphics. In physics, scalar multiplication is used to calculate the work done by a force. In engineering, scalar multiplication is used to calculate the moment of a force. In computer graphics, scalar multiplication is used to scale and rotate objects.
Scalar multiplication is a fundamental operation that is used in a wide variety of applications. It is essential for understanding the behavior of vectors and for solving problems in physics, engineering, and computer graphics.
Dot product
The dot product is a mathematical operation that takes two vectors as input and produces a scalar as output. The dot product is often used to calculate the angle between two vectors or the projection of one vector onto another.
In the context of i j k vectors, the dot product is defined as follows:
$$\mathbf{a} \cdot \mathbf{b} = a_1 b_1 + a_2 b_2 + a_3 b_3$$ where $\mathbf{a} = (a_1, a_2, a_3)$ and $\mathbf{b} = (b_1, b_2, b_3)$ are two i j k vectors.The dot product has a number of important properties. First, the dot product is commutative, which means that $\mathbf{a} \cdot \mathbf{b} = \mathbf{b} \cdot \mathbf{a}$. Second, the dot product is distributive over vector addition, which means that $\mathbf{a} \cdot (\mathbf{b} + \mathbf{c}) = \mathbf{a} \cdot \mathbf{b} + \mathbf{a} \cdot \mathbf{c}$. Third, the dot product of a vector with itself is equal to the square of the vector's magnitude, which means that $\mathbf{a} \cdot \mathbf{a} = \|\mathbf{a}\|^2$.
The dot product is a powerful tool that can be used to solve a variety of problems in physics, engineering, and computer graphics. For example, the dot product can be used to calculate the angle between two vectors, the projection of one vector onto another, and the work done by a force.
Cross product
The cross product is a mathematical operation that takes two vectors as input and produces a vector as output. The cross product is often used to calculate the area of a parallelogram or the volume of a parallelepiped. In the context of i j k vectors, the cross product is defined as follows:
$$\mathbf{a} \times \mathbf{b} = (a_2 b_3 - a_3 b_2, a_3 b_1 - a_1 b_3, a_1 b_2 - a_2 b_1)$$ where $\mathbf{a} = (a_1, a_2, a_3)$ and $\mathbf{b} = (b_1, b_2, b_3)$ are two i j k vectors.- Calculating the area of a parallelogram
The cross product can be used to calculate the area of a parallelogram. The area of a parallelogram is equal to the magnitude of the cross product of two vectors that are parallel to the sides of the parallelogram.
- Calculating the volume of a parallelepiped
The cross product can be used to calculate the volume of a parallelepiped. The volume of a parallelepiped is equal to the magnitude of the cross product of three vectors that are parallel to the sides of the parallelepiped.
- Applications
The cross product is used in a variety of applications, including physics, engineering, and computer graphics. In physics, the cross product is used to calculate the torque on an object. In engineering, the cross product is used to calculate the moment of a force. In computer graphics, the cross product is used to calculate the normal vector to a surface.
The cross product is a powerful tool that can be used to solve a variety of problems in physics, engineering, and computer graphics. It is essential for understanding the behavior of vectors and for solving problems in three-dimensional space.
FAQs about "i j k vector"
i j k vectors are a fundamental concept in linear algebra and have a wide range of applications in various fields such as physics, engineering, and computer graphics. Here are some frequently asked questions about i j k vectors:
Question 1: What is an i j k vector?
Answer: An i j k vector is an ordered triple of numbers that represent the coordinates of a point in three-dimensional space. The letters "i", "j", and "k" are used to represent the unit vectors in the x, y, and z directions, respectively.
Question 2: How do you add and subtract i j k vectors?
Answer: To add two i j k vectors, you simply add their corresponding coordinates. To subtract one i j k vector from another, you simply subtract the corresponding coordinates.
Question 3: What is scalar multiplication?
Answer: Scalar multiplication is a mathematical operation that multiplies an i j k vector by a scalar. A scalar is a quantity that has only magnitude, not direction. Scalar multiplication can be used to scale an i j k vector or to change its direction.
Question 4: What is the dot product?
Answer: The dot product is a mathematical operation that takes two i j k vectors as input and produces a scalar as output. The dot product is often used to calculate the angle between two vectors or the projection of one vector onto another.
Question 5: What is the cross product?
Answer: The cross product is a mathematical operation that takes two i j k vectors as input and produces a vector as output. The cross product is often used to calculate the area of a parallelogram or the volume of a parallelepiped.
Question 6: What are some applications of i j k vectors?
Answer: i j k vectors are used in a wide range of applications, including physics, engineering, and computer graphics. In physics, i j k vectors are used to represent forces, velocities, and positions. In engineering, i j k vectors are used to represent forces, moments, and stresses. In computer graphics, i j k vectors are used to represent points, lines, and polygons.
These are just a few of the most frequently asked questions about i j k vectors. For more information, please refer to a textbook on linear algebra or consult with a qualified professional.
Thank you for reading.
Conclusion
In this article, we have explored the concept of "i j k vector" and its various applications in different fields.
We have seen that i j k vectors are a powerful tool for representing and manipulating points in three-dimensional space. They can be used to perform a variety of operations, such as vector addition, subtraction, scalar multiplication, dot product, and cross product. These operations can be used to solve a wide range of problems in physics, engineering, and computer graphics.
As we move forward, i j k vectors will continue to play an important role in various fields. With the increasing use of computers in science and engineering, the demand for skilled professionals who can use i j k vectors to solve complex problems will only grow.
Unlock Seamless Git Collaborations: How To Use SSH Keys With Sourcetree
Ultimate Guide To King Size Bed Sheets Measurements In Centimeters
Unveiling Kawasaki's Revolutionary Cyclonic Engine: Engineering Marvel Unveiled
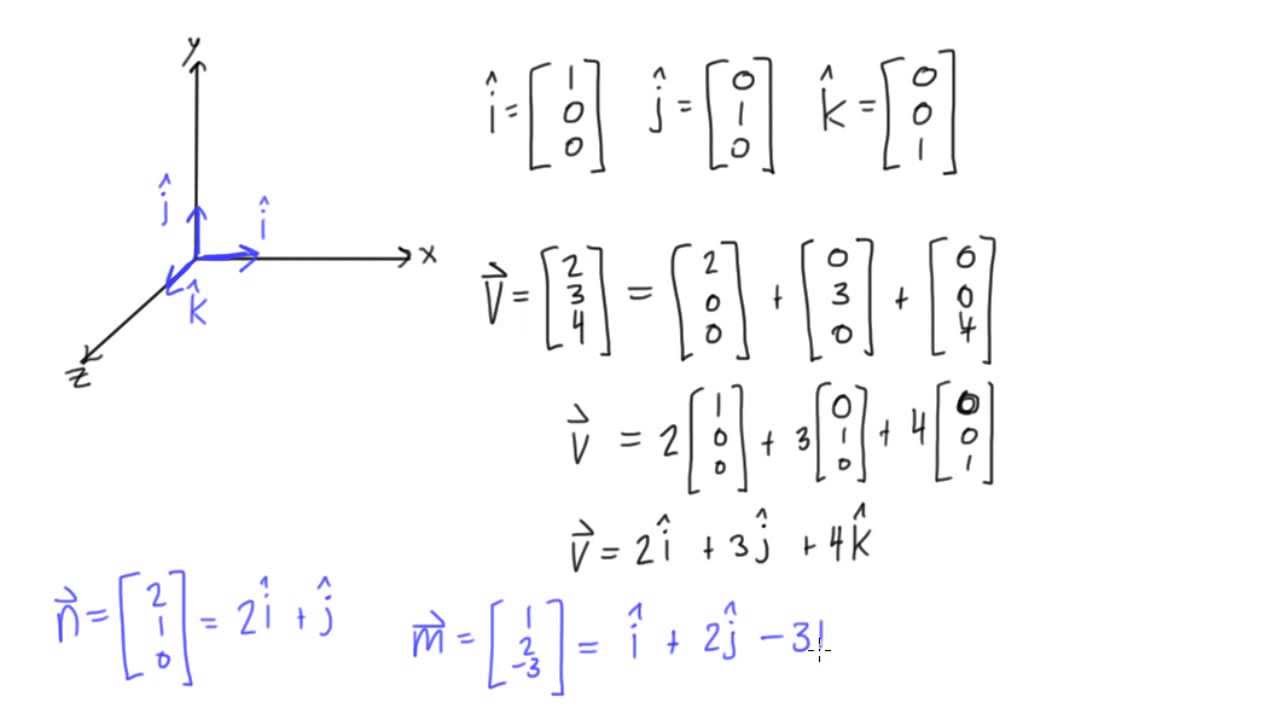
Using i, j, k unit vectors to express vectors YouTube

Vectors (Part9) i j k Unit Vectors, IITJEE physics classes YouTube

Misc 18 (MCQ) The value of i.(j x k) + j.(i x k) + k.(i x j) is