How many nets are there for a square-based pyramid?
A net is a two-dimensional representation of a three-dimensional object. It is made up of the faces of the object, laid out flat. A square-based pyramid has 5 faces: a square base and 4 triangular faces. To make a net for a square-based pyramid, you need to draw the square base and then draw the 4 triangles that make up the sides. The triangles should be attached to the base along one of their sides.There are 11 different nets that can be created for a square-based pyramid. They are all made up of the same 5 faces, but the arrangement of the faces is different. Some nets are easier to fold into a pyramid than others.Nets are important because they allow us to understand the three-dimensional structure of an object. They can also be used to create models of objects.
Here are some of the benefits of using nets:
- Nets are a simple way to represent complex three-dimensional objects.
- Nets can be used to create models of objects, which can be helpful for understanding their structure and function.
- Nets can be used to calculate the surface area and volume of objects.
Nets have been used for centuries to design and build objects. They are still used today in a variety of fields, including architecture, engineering, and manufacturing.
How many nets for square based pyramid
Understanding the concept of nets for a square-based pyramid involves exploring several key aspects:
- Number of faces: A square-based pyramid has 5 faces - 1 square base and 4 triangular sides.
- Net arrangement: The arrangement of faces in a net determines its foldability into a pyramid.
- Surface area: The net's surface area is equal to the total surface area of the pyramid it represents.
- Volume: The net's shape influences the volume of the resulting pyramid.
- Geometric properties: Nets reveal insights into the pyramid's geometric properties, such as its height and base dimensions.
- Practical applications: Nets are used in architecture, engineering, and packaging to design and represent three-dimensional structures.
These aspects collectively provide a comprehensive understanding of nets for square-based pyramids. They highlight the relationship between the net's two-dimensional representation and the resulting three-dimensional pyramid, enabling us to analyze and manipulate such structures effectively.
Number of faces
The number of faces in a square-based pyramid directly influences the number and arrangement of nets that can be created for it. A net is a two-dimensional representation of a three-dimensional object, and it must include all of the object's faces. Since a square-based pyramid has 5 faces, any net for this pyramid must also have 5 faces - 1 square and 4 triangles. The arrangement of these faces determines the specific net pattern.
For example, one common net for a square-based pyramid has the square base at the bottom, with the four triangular faces arranged around it in a symmetrical pattern. Another net has the square base on one side, with the triangular faces arranged in a more complex pattern on the other side. Each net represents the same pyramid, but the arrangement of the faces affects the ease of folding and assembly.
Understanding the relationship between the number of faces in a square-based pyramid and the number of nets that can be created for it is important for several reasons. First, it allows us to determine how many different nets are possible for a given pyramid. Second, it helps us to understand the relationship between the two-dimensional net and the three-dimensional pyramid it represents. Finally, it can help us to design and create nets for square-based pyramids for various applications, such as packaging, architecture, and engineering.
Net arrangement
In the context of "how many nets for square based pyramid", the arrangement of faces in a net is crucial because it directly affects the number of possible nets and their foldability into a three-dimensional pyramid. Each unique arrangement of faces results in a different net pattern, and some arrangements may be more difficult to fold into a pyramid than others.
- Foldability: The arrangement of faces in a net determines how easily it can be folded into a pyramid. Some arrangements may require complex folds or cuts, while others may be easier to fold. The foldability of a net is important for practical applications, such as packaging and origami.
- Number of nets: The number of possible nets for a given square-based pyramid depends on the arrangement of faces. Different arrangements can result in different nets, even though they represent the same pyramid.
- Symmetry: The arrangement of faces in a net can affect the symmetry of the resulting pyramid. Symmetrical nets produce symmetrical pyramids, while asymmetric nets produce asymmetric pyramids. Symmetry is an important consideration in many applications, such as architecture and design.
- Stability: The arrangement of faces in a net can also affect the stability of the resulting pyramid. Some arrangements may result in pyramids that are more stable and less likely to collapse, while others may result in pyramids that are less stable and more prone to collapse. Stability is an important consideration in applications where the pyramid will be subjected to forces or loads.
Understanding the connection between net arrangement and foldability is essential for designing and creating nets for square-based pyramids. By carefully considering the arrangement of faces, it is possible to create nets that are easy to fold, produce symmetrical pyramids, and are stable enough for the intended application.
Surface area
The surface area of a net is directly related to the total surface area of the pyramid it represents. This relationship is important because it allows us to calculate the surface area of a pyramid using the net. To calculate the surface area of a pyramid using the net, we simply need to find the area of the net and then multiply that area by the number of faces in the pyramid. For example, if the net has an area of 10 square units and the pyramid has 5 faces, then the total surface area of the pyramid is 50 square units.
Understanding the relationship between the surface area of a net and the surface area of the pyramid it represents is important for several reasons. First, it allows us to quickly and easily calculate the surface area of a pyramid. Second, it helps us to understand the relationship between the two-dimensional net and the three-dimensional pyramid it represents. Finally, it can help us to design and create nets for pyramids that have specific surface area requirements.
For example, in the field of packaging, it is important to design nets that have a specific surface area in order to accommodate the product inside. By understanding the relationship between the surface area of a net and the surface area of the pyramid it represents, we can design nets that meet the specific requirements of the product and the packaging process.
Volume
The shape of a net directly influences the volume of the resulting pyramid. This relationship is important because it allows us to design nets that will produce pyramids with specific volumes. For example, if we want to create a pyramid with a large volume, we need to use a net that has a large surface area. Conversely, if we want to create a pyramid with a small volume, we need to use a net that has a small surface area.
- Surface area: The surface area of a net is directly related to the volume of the resulting pyramid. The larger the surface area of the net, the larger the volume of the pyramid. This is because the surface area of the net determines the amount of material that is available to form the pyramid.
- Shape: The shape of the net also influences the volume of the resulting pyramid. Nets that are more symmetrical and regular will produce pyramids with larger volumes than nets that are more irregular and asymmetrical. This is because symmetrical and regular nets can be folded more efficiently, which results in a pyramid with a more compact shape and a larger volume.
- Height: The height of the pyramid is also influenced by the shape of the net. Nets that are taller and narrower will produce pyramids with larger volumes than nets that are shorter and wider. This is because taller and narrower nets can be folded into pyramids with steeper sides, which results in a pyramid with a larger volume.
Understanding the relationship between the shape of a net and the volume of the resulting pyramid is important for several reasons. First, it allows us to design nets that will produce pyramids with specific volumes. Second, it helps us to understand the relationship between the two-dimensional net and the three-dimensional pyramid it represents. Finally, it can help us to create nets for pyramids that are used in a variety of applications, such as architecture, engineering, and packaging.
Geometric properties
In the context of "how many nets for square based pyramid", understanding the geometric properties that nets reveal is crucial. Nets provide valuable insights into the pyramid's height and base dimensions, which are essential factors in determining the pyramid's overall shape and volume.
- Height: Nets disclose the height of the pyramid, which is the vertical distance from the base to the apex. By analyzing the net's shape and dimensions, we can determine the pyramid's height without having to construct the actual pyramid.
- Base dimensions: Nets also reveal the dimensions of the pyramid's base, such as its length and width. These dimensions provide information about the pyramid's stability and its ability to withstand external forces.
- Symmetry: Nets can indicate the symmetry of the pyramid. Symmetrical nets produce pyramids with regular shapes, while asymmetrical nets produce pyramids with irregular shapes. Understanding the symmetry of the net helps in predicting the pyramid's overall appearance and its aesthetic appeal.
- Volume: While nets do not directly provide the volume of the pyramid, they offer insights that can aid in volume calculations. By analyzing the net's surface area and shape, we can estimate the volume of the resulting pyramid.
In conclusion, nets serve as valuable tools for understanding the geometric properties of square-based pyramids. They provide information about the pyramid's height, base dimensions, symmetry, and volume, which are essential factors in various applications, including architecture, engineering, and design.
Practical applications
Understanding the concept of nets for square-based pyramids extends beyond theoretical analysis; it finds practical applications in diverse fields such as architecture, engineering, and packaging. Nets serve as crucial tools in designing and representing three-dimensional structures, enabling professionals to visualize and plan complex projects.
In architecture, nets are employed to design buildings, bridges, and other structures. Architects utilize nets to create models and blueprints, allowing them to explore different design options and ensure structural stability. Nets help architects visualize the spatial relationships between various components, facilitating efficient and precise construction processes.
In engineering, nets are used to design and analyze complex structures such as bridges, roofs, and aircraft. Engineers rely on nets to calculate forces, stresses, and deformations, ensuring the safety and integrity of structures. Nets enable engineers to optimize designs, reduce material usage, and enhance structural performance.
In packaging, nets are essential for designing containers, boxes, and other packaging solutions. Packaging engineers use nets to create prototypes and test different designs, ensuring that products are protected during transportation and storage. Nets allow for efficient material usage, cost optimization, and improved product presentation.
In summary, understanding the concept of nets for square-based pyramids has practical significance in various industries. Nets serve as valuable tools for designing and representing three-dimensional structures, enabling professionals to visualize, analyze, and optimize complex projects in architecture, engineering, and packaging.
FAQs on "How Many Nets for Square Based Pyramid"
This section addresses commonly asked questions and misconceptions regarding nets for square-based pyramids, providing concise and informative answers.
Question 1: How many nets can be created for a square-based pyramid?
Answer: There are 11 distinct nets that can be created for a square-based pyramid. These nets vary in the arrangement of the square base and four triangular faces, but they all represent the same three-dimensional pyramid.
Question 2: What factors determine the number of nets for a square-based pyramid?
Answer: The number of faces and the arrangement of those faces influence the number of nets that can be created for a square-based pyramid.
Question 3: How does the net's surface area relate to the pyramid's surface area?
Answer: The surface area of the net is directly proportional to the total surface area of the square-based pyramid it represents. This relationship allows for easy calculation of the pyramid's surface area using the net.
Question 4: How does the net's shape affect the pyramid's volume?
Answer: The shape of the net influences the volume of the resulting pyramid. Nets with larger surface areas tend to produce pyramids with larger volumes.
Question 5: What practical applications exist for nets of square-based pyramids?
Answer: Nets are widely used in architecture, engineering, and packaging. Architects employ nets to design buildings and bridges, engineers use them to analyze structural stability, and packaging designers utilize nets to create containers and boxes.
Question 6: How can nets help visualize and analyze three-dimensional structures?
Answer: Nets provide a two-dimensional representation of three-dimensional objects, making it easier to visualize and understand their spatial relationships and properties. Engineers and architects use nets to analyze forces, stresses, and deformations in structures.
Summary: Understanding nets for square-based pyramids involves exploring the number of nets, their relationship to the pyramid's surface area and volume, and their practical applications. Nets serve as valuable tools for visualizing, designing, and analyzing three-dimensional structures in fields such as architecture, engineering, and packaging.
Transition to the next article section: This comprehensive overview of nets for square-based pyramids provides a foundation for further exploration into their geometric properties and applications.
Conclusion
In summary, the concept of nets for square-based pyramids encompasses various aspects, including the number of nets, their relationship to the pyramid's surface area and volume, and their practical applications. We have explored these aspects in detail, highlighting the significance of nets in visualizing, designing, and analyzing three-dimensional structures.
Understanding nets for square-based pyramids provides a foundation for further exploration into the realm of geometry and its applications. By delving deeper into the geometric properties of nets and their role in representing three-dimensional objects, we can unlock new possibilities in fields such as architecture, engineering, and packaging.
Watch Calcio TW Online For Free: Your Ultimate Guide To Streaming Soccer
The Rise Of Realism: Exploring The Profound Impact Of "Realismo Movimiento"
Efficient Catalytic Kerosene Heaters For Optimal Warmth

Square Based Pyramid GCSE Maths Steps & Examples
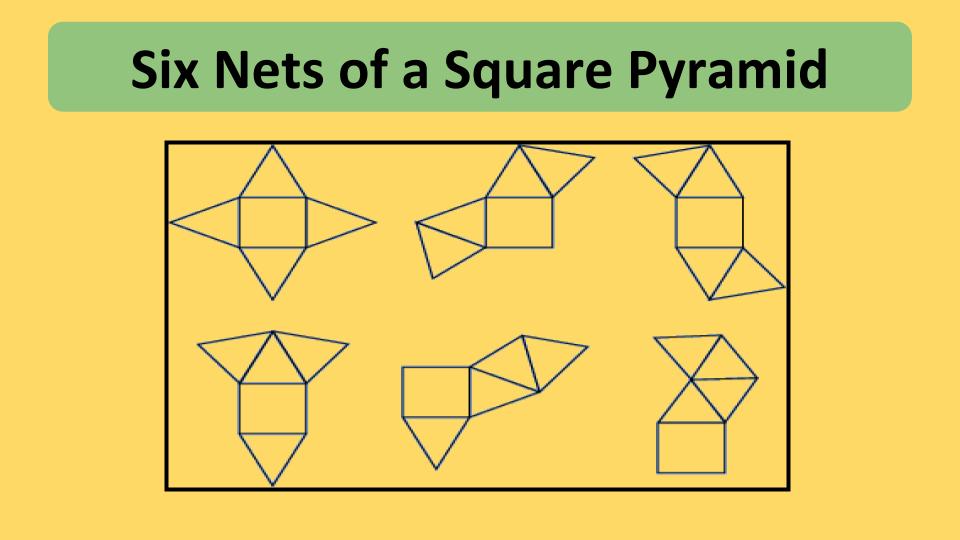
Ms Rashid Geometry Possible Nets for a Square Pyramid
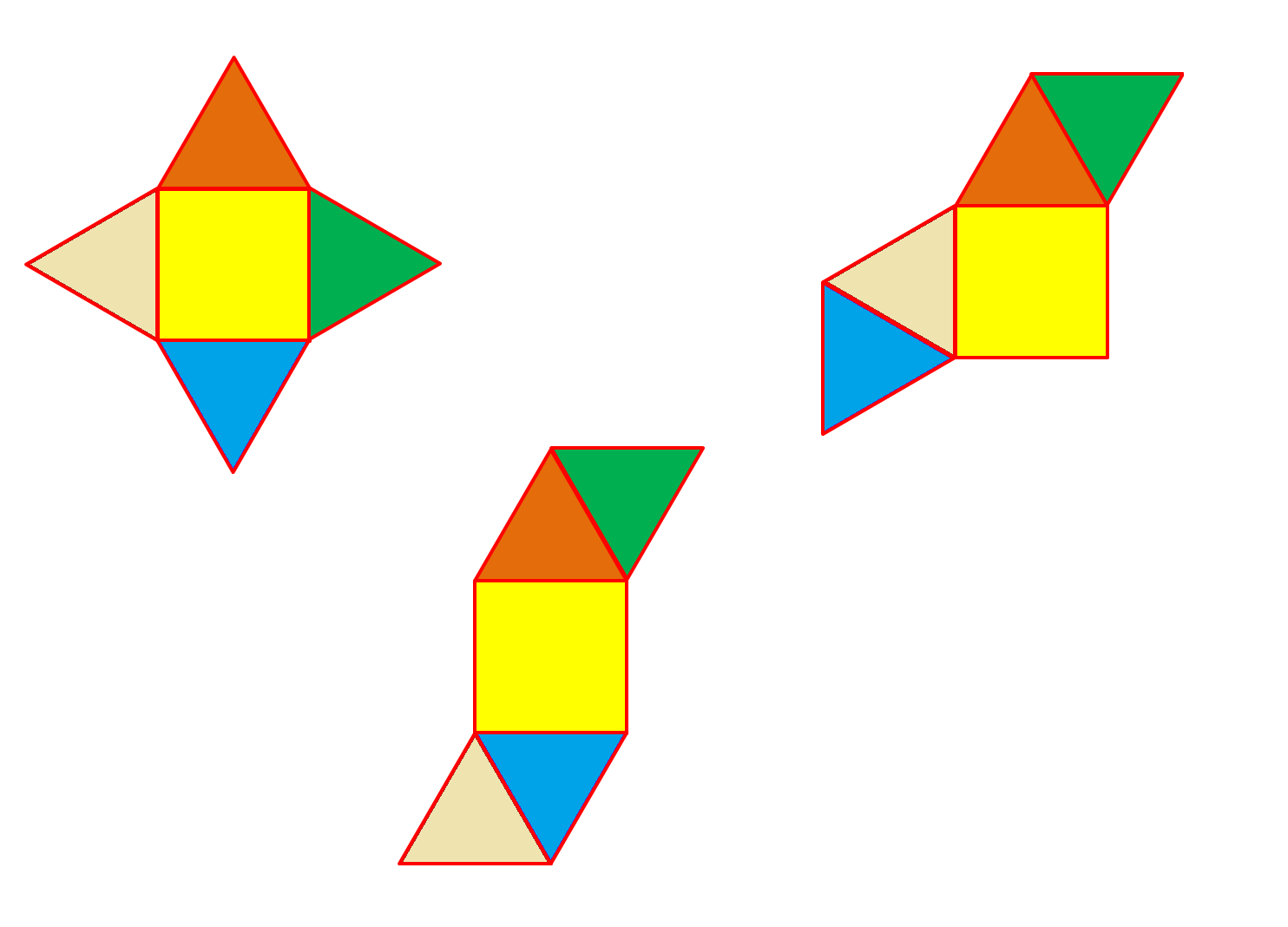
MEDIAN Don Steward mathematics teaching other numbers of nets